Radicación Algebraica.
1.1 Raíz cuadrada.
La raíz cuadrada enésima de un número real a es un número real b, si y sólo si la enésima potencia de b es a. Es decir.
Si y sólo si, b=a con a, b € R y n € z+
El número n recibe nombre de índice de la raíz, a es el radicando o cantidad subradical y b es la raíz.
Si n es par, se debe tener a >0 y b >0
Cuando en un raíz no aparece indicado el índice se debe entender que se refiere a una raíz cuadrada y dicho índice es 2. Además, recuerda que todo número real no negativo tiene una raíz cuadrada.
2. Radicación en los reales.
Reglas de la radicales.
1. Potencia enésima de la raíz enésima.
Si a pertenecer al conjunto de los números y n es un número entero positivo, se cumple que:
2. Raíz enésima de un producto.
Si a y b pertenecen al conjunto de los números reales y n es un número entero positivo }, se cumple que:
3. Raíz enésima de un cociente.
Si a y b pertenecen al conjunto de los números reales y n es un número entero positivo, se cumple que:
4. Raíz enésima de una potencia enésima.
Si a pertenece al conjunto de los número reales; n y m son números enteros positivos, se cumple que
Esto significa que la potencia de una raíz del radicando elevado a la potencia.
5. Raíz enésima de otra raíz enésima.
Si a pertenecer al conjunto de los números reales: n y m son número enteros positivos, entonces se cumple que
Esto significa que el índice de la raíz enésima de una raíz n-ésima se obtiene multiplicando los índices de los radicales y el radicando es el mismo.







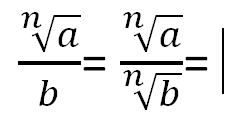


No hay comentarios:
Publicar un comentario